banner



Home  ›  Is Helium An Ideal Gas

Is Helium An Ideal Gas

Written By Wednesday, November 2, 2022 Add Comment Edit

Chapter three. The Offset Law of Thermodynamics

3.six Adiabatic Processes for an Ideal Gas

Learning Objectives

By the end of this section, you will be able to:

  • Ascertain adiabatic expansion of an ideal gas
  • Demonstrate the qualitative difference between adiabatic and isothermal expansions

When an ideal gas is compressed adiabatically [latex]\left(Q=0\right),[/latex] work is done on it and its temperature increases; in an adiabatic expansion, the gas does work and its temperature drops. Adiabatic compressions actually occur in the cylinders of a car, where the compressions of the gas-air mixture have place then quickly that there is no fourth dimension for the mixture to exchange heat with its environment. All the same, because work is done on the mixture during the compression, its temperature does rise significantly. In fact, the temperature increases tin be so large that the mixture can explode without the addition of a spark. Such explosions, since they are not timed, make a motorcar run poorly—it usually "knocks." Because ignition temperature rises with the octane of gasoline, i way to overcome this problem is to use a higher-octane gasoline.

Some other interesting adiabatic process is the gratis expansion of a gas. Figure 3.13 shows a gas confined by a membrane to ane side of a two-compartment, thermally insulated container. When the membrane is punctured, gas rushes into the empty side of the container, thereby expanding freely. Because the gas expands "against a vacuum" [latex]\left(p=0\right)[/latex], it does no piece of work, and because the vessel is thermally insulated, the expansion is adiabatic. With [latex]Q=0[/latex] and [latex]W=0[/latex] in the starting time constabulary, [latex]\text{Δ}{Eastward}_{\text{int}}=0,[/latex] so [latex]{Due east}_{\text{int}}{}_{i}={E}_{\text{int}}{}_{f}[/latex] for the free expansion.

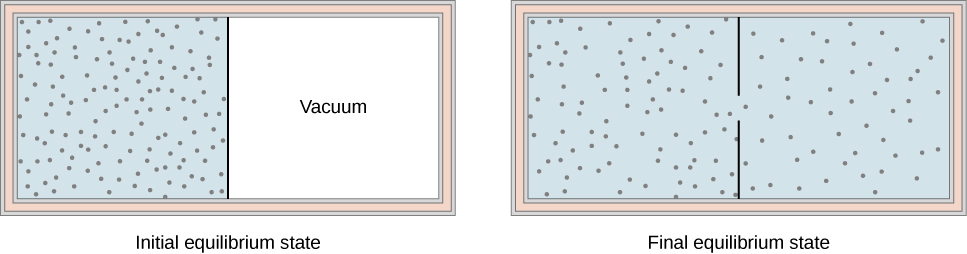
The figure on the left is an illustration of the initial equilibrium state of a container with a partition in the middle dividing it into two chambers. The outer walls are insulated. The chamber on the left is full of gas, indicated by blue shading and many small dots representing the gas molecules. The right chamber is empty. The figure on the right is an illustration of the final equilibrium state of the container. The partition has a hole in it. The entire container, on both sides of the partition, is full of gas, indicated by blue shading and many small dots representing the gas molecules. The dots in the second, final equilibrium state, illustration are less dense than in the first, initial state illustration.
Figure iii.13 The gas in the left chamber expands freely into the correct sleeping room when the membrane is punctured.

If the gas is ideal, the internal free energy depends only on the temperature. Therefore, when an ideal gas expands freely, its temperature does non modify.

A quasi-static, adiabatic expansion of an ideal gas is represented in Effigy 3.fourteen, which shows an insulated cylinder that contains one mol of an platonic gas. The gas is fabricated to expand quasi-statically by removing one grain of sand at a time from the summit of the piston. When the gas expands by dV, the change in its temperature is dT. The work washed by the gas in the expansion is [latex]dW=pdV;dQ=0[/latex] considering the cylinder is insulated; and the change in the internal energy of the gas is, from Equation 3.9, [latex]d{E}_{\text{int}}={C}_{V}dT.[/latex] Therefore, from the first law,

[latex]{C}_{Five}dT=0-pdV=\text{−}pdV,[/latex]

so

[latex]dT=-\frac{pdV}{{C}_{V}}.[/latex]

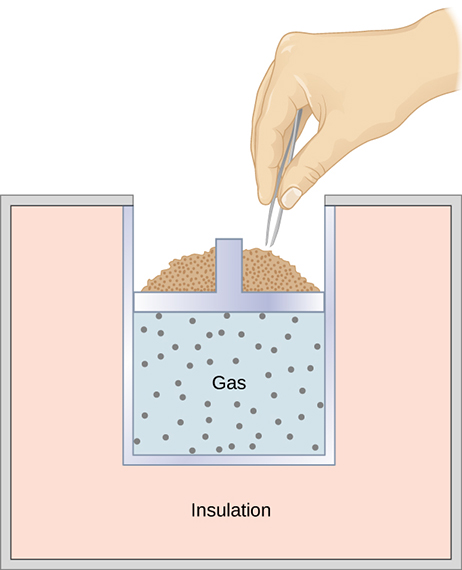
The figure is an illustration of a container. The walls and bottom are filled with a thick layer of insulation. The chamber of the container is closed from above by a piston. Inside the chamber is a gas. There is a pile of sand on top of the piston, and a hand with tweezers is removing grains from the pile.
Effigy 3.14 When sand is removed from the piston ane grain at a time, the gas expands adiabatically and quasi-statically in the insulated vessel.

As well, for 1 mol of an platonic gas,

[latex]d\left(pV\right)=d\left(RT\right),[/latex]

so

[latex]pdV+Vdp=RdT[/latex]

and

[latex]dT=\frac{pdV+Vdp}{R}.[/latex]

Nosotros at present accept 2 equations for dT. Upon equating them, we observe that

[latex]{C}_{V}Vdp+\left({C}_{5}+R\right)pdV=0.[/latex]

Now, we dissever this equation by pV and apply [latex]{C}_{p}={C}_{V}+R[/latex]. Nosotros are then left with

[latex]{C}_{5}\frac{dp}{p}+{C}_{p}\frac{dV}{V}=0,[/latex]

which becomes

[latex]\frac{dp}{p}+\gamma \frac{dV}{V}=0,[/latex]

where nosotros define [latex]\text{γ}[/latex] as the ratio of the molar oestrus capacities:

[latex]\gamma =\frac{{C}_{p}}{{C}_{V}}.[/latex]

Thus,

[latex]\int \frac{dp}{p}+\gamma \int \frac{dV}{Five}=0[/latex]

and

[latex]\text{ln}\phantom{\rule{0.2em}{0ex}}p+\text{γ}\text{ln}\phantom{\rule{0.2em}{0ex}}V=\text{abiding}\text{.}[/latex]

Finally, using [latex]\text{ln}\left({A}^{10}\right)=ten\text{ln}A\phantom{\dominion{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}\text{ln}\phantom{\rule{0.2em}{0ex}}AB=\text{ln}\phantom{\rule{0.2em}{0ex}}A+\text{ln}\phantom{\rule{0.2em}{0ex}}B[/latex], we can write this in the grade

[latex]p{5}^{\gamma }=\text{abiding}\text{.}[/latex]

This equation is the status that must exist obeyed by an platonic gas in a quasi-static adiabatic process. For example, if an ideal gas makes a quasi-static adiabatic transition from a state with pressure and book [latex]{p}_{1}[/latex] and [latex]{V}_{1}[/latex] to a state with [latex]{p}_{2}[/latex] and [latex]{V}_{ii},[/latex] then it must be truthful that [latex]{p}_{1}{V}_{1}^{\gamma }={p}_{2}{Five}_{two}^{\gamma }.[/latex]

The adiabatic condition of Effigy 3.12 tin can be written in terms of other pairs of thermodynamic variables by combining it with the platonic gas police. In doing this, we find that

[latex]{p}^{ane-\gamma }{T}^{\gamma }=\text{abiding}[/latex]

and

[latex]T{Five}^{\gamma -i}=\text{abiding}\text{.}[/latex]

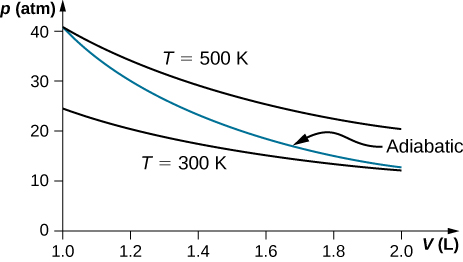
A reversible adiabatic expansion of an ideal gas is represented on the pV diagram of Figure 3.15. The slope of the curve at any indicate is

[latex]\frac{dp}{dV}=\frac{d}{dV}\left(\frac{\text{constant}}{{V}^{\gamma }}\right)=\text{−}\gamma \frac{p}{5}.[/latex]

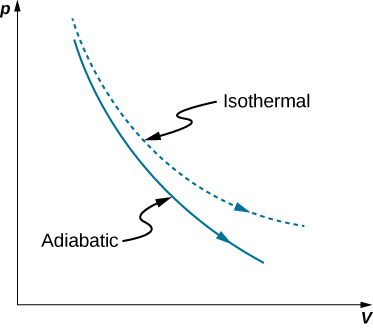
The figure is a plot of pressure, p on the vertical axis as a function of volume, V on the horizontal axis. Two curves are plotted. Both are monotonically decreasing and concave up. One is slightly higher and has a greater curvature. This curve is labeled
Figure 3.xv Quasi-static adiabatic and isothermal expansions of an platonic gas.

The dashed curve shown on this pV diagram represents an isothermal expansion where T (and therefore pV) is constant. The slope of this curve is useful when we consider the 2nd law of thermodynamics in the next chapter. This slope is

[latex]\frac{dp}{dV}=\frac{d}{dV}\phantom{\dominion{0.2em}{0ex}}\frac{nRT}{V}=-\frac{p}{Five}.[/latex]

Because [latex]\text{γ}>1,[/latex] the isothermal curve is not equally steep as that for the adiabatic expansion.

Case

Compression of an Ideal Gas in an Automobile Engine

Gasoline vapor is injected into the cylinder of an automobile engine when the piston is in its expanded position. The temperature, pressure, and volume of the resulting gas-air mixture are [latex]twenty\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], [latex]one.00\phantom{\dominion{0.2em}{0ex}}×\phantom{\dominion{0.2em}{0ex}}{10}^{5}{\phantom{\rule{0.2em}{0ex}}\text{Due north/1000}}^{ii}\text{,}[/latex] and [latex]240{\phantom{\dominion{0.2em}{0ex}}\text{cm}}^{3}[/latex], respectively. The mixture is then compressed adiabatically to a volume of [latex]xl{\phantom{\rule{0.2em}{0ex}}\text{cm}}^{iii}[/latex]. Note that in the actual performance of an machine engine, the compression is not quasi-static, although we are making that supposition hither. (a) What are the pressure and temperature of the mixture afterward the compression? (b) How much work is done by the mixture during the compression?

Strategy

Because we are modeling the procedure as a quasi-static adiabatic pinch of an platonic gas, we have [latex]p{V}^{\gamma }=\phantom{\rule{0.2em}{0ex}}\text{constant}[/latex] and [latex]pV=nRT[/latex]. The work needed can then be evaluated with [latex]Westward={\int }_{{Five}_{1}}^{{V}_{2}}pdV[/latex].

Solution

Show Answer
  1. For an adiabatic compression we take

    [latex]{p}_{2}={p}_{1}{\left(\frac{{V}_{1}}{{V}_{2}}\right)}^{\gamma },[/latex]


     so after the compression, the force per unit area of the mixture is

    [latex]{p}_{2}=\left(1.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{five}{\phantom{\rule{0.2em}{0ex}}\text{N/one thousand}}^{two}\correct){\left(\frac{240\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{ten}^{-6}{\phantom{\rule{0.2em}{0ex}}\text{m}}^{3}}{xl\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{ten}^{-half dozen}{\phantom{\rule{0.2em}{0ex}}\text{grand}}^{3}}\correct)}^{1.40}=ane.23\phantom{\rule{0.2em}{0ex}}×\phantom{\dominion{0.2em}{0ex}}{x}^{6}{\phantom{\rule{0.2em}{0ex}}\text{N/m}}^{2}\text{.}[/latex]


     From the platonic gas law, the temperature of the mixture after the compression is

    [latex]\begin{assortment}{cc}\hfill {T}_{ii}& =\left(\frac{{p}_{two}{5}_{2}}{{p}_{ane}{V}_{i}}\right){T}_{1}\hfill \\ & =\frac{\left(i.23\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{6}{\phantom{\dominion{0.2em}{0ex}}\text{Northward/m}}^{ii}\right)\left(xl\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-half dozen}{\phantom{\dominion{0.2em}{0ex}}\text{m}}^{3}\right)}{\left(1.00\phantom{\rule{0.2em}{0ex}}×\phantom{\dominion{0.2em}{0ex}}{10}^{5}{\phantom{\dominion{0.2em}{0ex}}\text{N/grand}}^{ii}\correct)\left(240\phantom{\dominion{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{ten}^{-6}{\phantom{\rule{0.2em}{0ex}}\text{grand}}^{iii}\right)}·293\phantom{\dominion{0.2em}{0ex}}\text{K}\hfill \\ & =600\phantom{\rule{0.2em}{0ex}}\text{K}=328\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}\text{.}\hfill \end{array}[/latex]

  2. The work washed by the mixture during the compression is

    [latex]W={\int }_{{5}_{1}}^{{V}_{2}}pdV.[/latex]


     With the adiabatic condition of Equation three.12, nosotros may write p as [latex]Yard\text{/}{V}^{\text{γ}},[/latex] where [latex]K={p}_{1}{V}_{1}^{\gamma }={p}_{two}{V}_{2}^{\gamma }.[/latex] The work is therefore

    [latex]\begin{array}{cc}\hfill W& \phantom{\rule{0.2em}{0ex}}={\int }_{{Five}_{one}}^{{V}_{2}}\frac{K}{{5}^{\gamma }}dV\hfill \\ & \phantom{\dominion{0.2em}{0ex}}=\frac{Grand}{ane-\gamma }\left(\frac{1}{{V}_{ii}{}^{\gamma -1}}-\frac{1}{{V}_{one}{}^{\gamma -1}}\right)\hfill \\ & =\phantom{\dominion{0.2em}{0ex}}\frac{1}{1-\gamma }\left(\frac{{p}_{2}{V}_{two}^{\gamma }}{{V}_{2}{}^{\gamma -ane}}-\frac{{p}_{1}{Five}_{1}^{\gamma }}{{V}_{1}{}^{\gamma -1}}\right)\hfill \\ & =\phantom{\rule{0.2em}{0ex}}\frac{1}{ane-\gamma }\left({p}_{2}{5}_{2}-{p}_{one}{5}_{1}\right)\hfill \\ & \phantom{\rule{0.2em}{0ex}}=\frac{i}{one-1.40}\left[\left(ane.23\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{six}\phantom{\dominion{0.2em}{0ex}}{\text{N/one thousand}}^{ii}\correct)\left(twoscore\phantom{\dominion{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{ten}^{-half dozen}\phantom{\dominion{0.2em}{0ex}}{\text{k}}^{3}\correct) \\  -\left(1.00\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{5}\phantom{\rule{0.2em}{0ex}}{\text{North/grand}}^{2}\correct)\left(240\phantom{\rule{0.2em}{0ex}}×\phantom{\dominion{0.2em}{0ex}}{10}^{-6}{\text{thousand}}^{3}\right)\right]\hfill \\ & \phantom{\rule{0.2em}{0ex}}=-63\phantom{\dominion{0.2em}{0ex}}\text{J}\text{.}\hfill \end{array}[/latex]

Significance

The negative sign on the work done indicates that the piston does work on the gas-air mixture. The engine would not work if the gas-air mixture did work on the piston.

Summary

  • A quasi-static adiabatic expansion of an ideal gas produces a steeper pV curve than that of the corresponding isotherm.
  • A realistic expansion tin can exist adiabatic but rarely quasi-static.

Cardinal Equations

Equation of country for a closed system [latex]f\left(p,V,T\right)=0[/latex]
Net work for a finite change in volume [latex]W={\int }_{{5}_{i}}^{{V}_{2}}pdV[/latex]
Internal energy of a system (average total free energy) [latex]{Eastward}_{\text{int}}=\sum _{i}\left({\overline{Thou}}_{i}+{\overline{U}}_{i}\right),[/latex]
Internal energy of a monatomic ideal gas [latex]{E}_{\text{int}}=n{N}_{\text{A}}\left(\frac{3}{two}{one thousand}_{\text{B}}T\right)=\frac{3}{2}nRT[/latex]
First police force of thermodynamics [latex]\text{Δ}{East}_{\text{int}}=Q-Westward[/latex]
Molar estrus capacity at constant pressure [latex]{C}_{p}={C}_{V}+R[/latex]
Ratio of molar heat capacities [latex]\gamma ={C}_{p}\text{/}{C}_{V}[/latex]
Condition for an ideal gas in a quasi-static adiabatic process [latex]p{V}^{\gamma }=\phantom{\rule{0.2em}{0ex}}\text{abiding}[/latex]

Conceptual Questions

Is it possible for [latex]\text{γ}[/latex] to be smaller than unity?

Show Solution

No, it is ever greater than 1.

Would yous expect [latex]\text{γ}[/latex] to exist larger for a gas or a solid? Explain.

There is no modify in the internal free energy of an platonic gas undergoing an isothermal process since the internal free energy depends only on the temperature. Is it therefore right to say that an isothermal process is the same every bit an adiabatic procedure for an platonic gas? Explain your answer.

Show Solution

An adiabatic procedure has a alter in temperature merely no heat flow. The isothermal process has no change in temperature but has heat flow.

Does a gas do any work when it expands adiabatically? If and then, what is the source of the energy needed to do this piece of work?

Problems

A monatomic platonic gas undergoes a quasi-static adiabatic expansion in which its book is doubled. How is the force per unit area of the gas changed?

Show Solution

pressure decreased by 0.31 times the original pressure level

An ideal gas has a pressure of 0.50 atm and a book of 10 L. It is compressed adiabatically and quasi-statically until its pressure level is 3.0 atm and its volume is ii.8 50. Is the gas monatomic, diatomic, or polyatomic?

Force per unit area and volume measurements of a dilute gas undergoing a quasi-static adiabatic expansion are shown below. Plot ln p vs. V and determine [latex]\text{γ}[/latex] for this gas from your graph.

P (atm) V (L)
20.0 1.0
17.0 ane.1
xiv.0 one.3
eleven.0 one.v
8.0 2.0
v.0 2.6
2.0 5.ii
1.0 8.4
Bear witness Solution

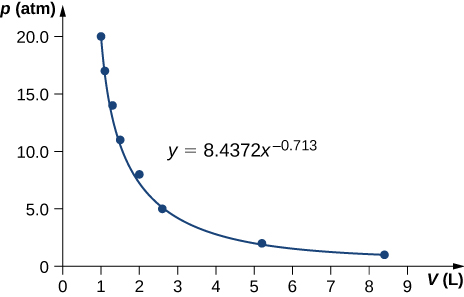
The figure is a plot of pressure, p, in atmospheres on the vertical axis as a function of volume, V, in liters on the horizontal axis. The horizontal volume scale runs from 0 to 20, and the vertical pressure scale runs from 0 to 9. The data from the previous table is plotted as points and the equation y equals 8.4372 x to the minus 0.713 power is plotted as a curve. The points all lie on or very close to the curve.

;
[latex]\gamma =0.713[/latex]

An platonic monatomic gas at 300 Chiliad expands adiabatically and reversibly to twice its book. What is its final temperature?

An ideal diatomic gas at 80 Yard is slowly expanded adiabatically and reversibly to twice its volume. What is its final temperature?

Show Solution

84 K

An ideal diatomic gas at eighty K is slowly compressed adiabatically to i-third its original volume. What is its last temperature?

Compare the charge in internal free energy of an ideal gas for a quasi-static adiabatic expansion with that for a quasi-static isothermal expansion. What happens to the temperature of an platonic gas in an adiabatic expansion?

Bear witness Solution

An adiabatic expansion has less work done and no heat flow, thereby a lower internal energy comparison to an isothermal expansion which has both estrus menstruum and work done. Temperature decreases during adiabatic expansion.

The temperature of n moles of an ideal gas changes from [latex]{T}_{1}[/latex] to [latex]{T}_{two}[/latex] in a quasi-static adiabatic transition. Evidence that the work washed past the gas is given by

[latex]W=\frac{nR}{\gamma -1}\left({T}_{1}-{T}_{2}\right).[/latex]

A dilute gas expands quasi-statically to three times its initial volume. Is the last gas pressure greater for an isothermal or an adiabatic expansion? Does your answer depend on whether the gas is monatomic, diatomic, or polyatomic?

Show Solution

Isothermal has a greater last pressure and does not depend on the type of gas.

(a) An ideal gas expands adiabatically from a book of [latex]2.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{x}^{-3}{\phantom{\rule{0.2em}{0ex}}\text{m}}^{3}[/latex] to [latex]two.5\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}{\phantom{\rule{0.2em}{0ex}}\text{m}}^{3}[/latex]. If the initial pressure and temperature were [latex]v.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{5}\phantom{\dominion{0.2em}{0ex}}\text{Pa}[/latex] and 300 K, respectively, what are the last pressure and temperature of the gas? Use [latex]\gamma =5\text{/}3[/latex] for the gas. (b) In an isothermal process, an ideal gas expands from a book of [latex]2.0\phantom{\rule{0.2em}{0ex}}×\phantom{\dominion{0.2em}{0ex}}{ten}^{-3}{\phantom{\rule{0.2em}{0ex}}\text{m}}^{3}[/latex] to [latex]2.v\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{ten}^{-3}{\phantom{\rule{0.2em}{0ex}}\text{k}}^{iii}[/latex]. If the initial pressure and temperature were [latex]v.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{5}\phantom{\rule{0.2em}{0ex}}\text{Pa}[/latex] and 300 G, respectively, what are the final pressure and temperature of the gas?

On an adiabatic procedure of an ideal gas pressure level, book and temperature modify such that [latex]p{5}^{\gamma }[/latex] is constant with [latex]\gamma =five\text{/}3[/latex] for monatomic gas such as helium and [latex]\gamma =7\text{/}5[/latex] for diatomic gas such as hydrogen at room temperature. Utilize numerical values to plot two isotherms of 1 mol of helium gas using ideal gas constabulary and two adiabatic processes mediating between them. Employ [latex]{T}_{1}=500\phantom{\rule{0.2em}{0ex}}\text{K},\phantom{\rule{0.2em}{0ex}}{V}_{ane}=ane\phantom{\rule{0.2em}{0ex}}\text{L},\phantom{\dominion{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}{T}_{two}=300\phantom{\rule{0.2em}{0ex}}\text{K}[/latex] for your plot.

Show Solution

The figure is a plot of pressure, p, in atmospheres on the vertical axis as a function of volume, V, in liters on the horizontal axis. The horizontal, V, axis runs from 1.0 to 2.0. The vertical, p, axis runs from 0 to about 40. Two isotherms are shown. One isotherm is for T equal to 500 K, with the pressure starting at about 40 atmospheres when the volume is 1.0 Liter and decreasing with volume to about 25 atmospheres at 2.0 liters. The second isotherm is for T equal to 300 K, with the pressure starting at about 25 atmospheres when the volume is 1.0 Liter and decreasing with volume to a little over 10 atmospheres at 2.0 liters. A third plot, labeled

Ii moles of a monatomic ideal gas such as helium is compressed adiabatically and reversibly from a state (3 atm, 5 Fifty) to a land with pressure iv atm. (a) Find the book and temperature of the final state. (b) Find the temperature of the initial state of the gas. (c) Notice the work done by the gas in the procedure. (d) Notice the alter in internal energy of the gas in the process.

Additional Bug

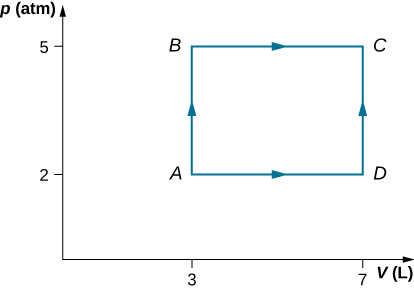
Consider the process shown beneath. During steps AB and BC, 3600 J and 2400 J of heat, respectively, are added to the system. (a) Observe the work done in each of the processes AB, BC, Advertizement, and DC. (b) Find the internal energy change in processes AB and BC. (c) Discover the internal energy difference between states C and A. (d) Observe the total heat added in the ADC procedure. (due east) From the information given, can yous find the estrus added in process Advertising? Why or why not?

The figure is a plot of pressure, p, in atmospheres on the vertical axis as a function of volume, V, in liters on the horizontal axis. The horizontal volume scale runs from 0 to 7, and the vertical pressure scale runs from 0 to 5. Four points, A, B, C, and D, are labeled on the plot and their pressures and volumes are labeled on the axes. Point A is at volume 3 L, pressure 2 atmospheres. Point B is at volume 3 L, pressure 5 atmospheres. Point C is at volume 7 L, pressure 5 atmospheres. Point D is at volume 7 L, pressure 2 atmospheres. A path goes from A up to B and across to C. Another path goes from A across to D and then up to C.

Show Solution

a. [latex]{W}_{AB}=0,{W}_{BC}=2026\phantom{\rule{0.2em}{0ex}}\text{J},{W}_{AD}=810.4\phantom{\rule{0.2em}{0ex}}\text{J},{W}_{DC}=0;[/latex] b. [latex]\text{Δ}{E}_{AB}=3600\phantom{\rule{0.2em}{0ex}}\text{J},\text{Δ}{East}_{BC}=374\phantom{\dominion{0.2em}{0ex}}\text{J;}[/latex] c. [latex]\text{Δ}{E}_{AC}=3974\phantom{\rule{0.2em}{0ex}}\text{J};[/latex] d. [latex]{Q}_{ADC}=4784\phantom{\rule{0.2em}{0ex}}\text{J;}[/latex] e. No, because heat was added for both parts AD and DC. There is not plenty data to figure out how much is from each segment of the path.

A car tire contains [latex]0.0380{\phantom{\dominion{0.2em}{0ex}}\text{grand}}^{3}[/latex] of air at a pressure of [latex]2.twenty\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{ten}^{five}\phantom{\rule{0.2em}{0ex}}\text{Pa}[/latex] (about 32 psi). How much more than internal energy does this gas have than the same volume has at cypher gauge force per unit area (which is equivalent to normal atmospheric pressure)?

A helium-filled toy balloon has a gauge pressure level of 0.200 atm and a volume of 10.0 Fifty. How much greater is the internal energy of the helium in the balloon than it would be at nix gauge pressure?

Bear witness Solution

300 J

Steam to drive an old-fashioned steam locomotive is supplied at a abiding gauge pressure of [latex]1.75\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{x}^{6}{\text{N/m}}^{2}[/latex] (about 250 psi) to a piston with a 0.200-grand radius. (a) By calculating [latex]p\text{Δ}V[/latex], notice the work done by the steam when the piston moves 0.800 thousand. Note that this is the net work output, since approximate pressure is used. (b) Now find the corporeality of piece of work by calculating the force exerted times the distance traveled. Is the answer the same equally in role (a)?

A hand-driven tire pump has a piston with a 2.50-cm diameter and a maximum stroke of 30.0 cm. (a) How much work do you do in one stroke if the average gauge pressure level is [latex]2.iv\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{v}{\phantom{\dominion{0.2em}{0ex}}\text{N/m}}^{2}[/latex] (nigh 35 psi)? (b) What average force practise you lot exert on the piston, neglecting friction and gravitational force?

Show Solution

a. 59.v J; b. 170 N

Calculate the internet work output of a heat engine following path ABCDA every bit shown below.

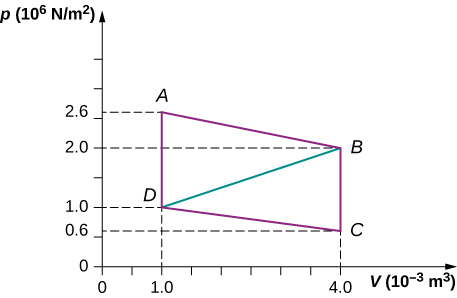
The figure is a plot of pressure, p, in nuits of 10 to the 6 Newtons per meter squared on the vertical axis as a function of volume, V, in 10 to the minus 3 cubic meters on the horizontal axis. The horizontal volume scale runs from 0 to 4, and the vertical pressure scale runs from 0 to about 4. Four points, A, B, C, and D, are labeled on the plot and their pressures and volumes are labeled on the axes. Point A is at volume 1.0 times 10 to the -3 cubic meters, pressure 2.6 times 10 to the 6 Newtons per meter squared. Point B is at volume 4.0 times 10 to the -3 cubic meters, pressure 2.0 times 10 to the 6 Newtons per meter squared. Point C is at volume 4.0 times 10 to the -3 cubic meters, pressure 0.6 times 10 to the 6 Newtons per meter squared. Point D is at volume 1.0 times 10 to the -3 cubic meters, pressure 1.0 times 10 to the 6 Newtons per meter squared. A straight line connects A to B, another straight line B to C, another straight line C to D, and another straight line back to A.

What is the net piece of work output of a heat engine that follows path ABDA in the preceding problem with a direct line from B to D? Why is the piece of work output less than for path ABCDA?

Show Solution

[latex]2.4\phantom{\dominion{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{iii}\phantom{\rule{0.2em}{0ex}}\text{J}[/latex]

5 moles of a monatomic ideal gas in a cylinder at [latex]27\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] is expanded isothermally from a volume of 5 L to 10 L. (a) What is the change in internal energy? (b) How much piece of work was washed on the gas in the procedure? (c) How much heat was transferred to the gas?

4 moles of a monatomic ideal gas in a cylinder at [latex]27\phantom{\dominion{0.2em}{0ex}}\text{°}\text{C}[/latex] is expanded at abiding pressure equal to 1 atm until its volume doubles. (a) What is the change in internal energy? (b) How much work was done by the gas in the procedure? (c) How much rut was transferred to the gas?

Show Solution

a. 15,000 J; b. ten,000 J; c. 25,000 J

Helium gas is cooled from [latex]20\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] to [latex]x\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] by expanding from 40 atm to 1 atm. If there is 1.iv mol of helium, (a) What is the final volume of helium? (b) What is the change in internal free energy?

In an adiabatic procedure, oxygen gas in a container is compressed along a path that tin be described by the post-obit pressure in atm equally a role of book V, with [latex]{V}_{0}=1L[/latex]: [latex]p=\left(three.0\phantom{\rule{0.2em}{0ex}}\text{atm}\correct)\left(V\text{/}{V}_{0}\right)^{-1.2}[/latex]. The initial and last volumes during the process were ii L and 1.five L, respectively. Observe the amount of work done on the gas.

Show Solution

78 J

A cylinder containing three moles of a monatomic platonic gas is heated at a constant pressure of ii atm. The temperature of the gas changes from 300 Yard to 350 K as a consequence of the expansion. Find work done (a) on the gas; and (b) by the gas.

A cylinder containing three moles of nitrogen gas is heated at a constant pressure of ii atm. The temperature of the gas changes from 300 K to 350 K as a result of the expansion. Find work done (a) on the gas, and (b) by the gas by using van der Waals equation of country instead of ideal gas law.

Show Solution

A cylinder containing three moles of nitrogen gas is heated at a constant pressure of 2 atm. a. −1220 J; b. +1220 J

Ii moles of a monatomic ideal gas such as oxygen is compressed adiabatically and reversibly from a state (three atm, five Fifty) to a state with a pressure of iv atm. (a) Find the volume and temperature of the last state. (b) Discover the temperature of the initial state. (c) Observe work done by the gas in the process. (d) Observe the change in internal free energy in the process. Assume [latex]{C}_{V}=5R[/latex] and [latex]{C}_{p}={C}_{5}+R[/latex] for the diatomic platonic gas in the conditions given.

An insulated vessel contains 1.five moles of argon at two atm. The gas initially occupies a volume of 5 Fifty. As a result of the adiabatic expansion the pressure level of the gas is reduced to i atm. (a) Find the book and temperature of the concluding country. (b) Find the temperature of the gas in the initial country. (c) Find the work done by the gas in the process. (d) Discover the change in the internal energy of the gas in the procedure.

Testify Solution

a. 7.half-dozen L, 61.half dozen Chiliad; b. 81.iii K; c. [latex]3.63\phantom{\rule{0.2em}{0ex}}\text{50}·\text{atm}=367\phantom{\rule{0.2em}{0ex}}\text{J}[/latex]; d. −367 J

Claiming Bug

I mole of an ideal monatomic gas occupies a book of [latex]one.0\phantom{\rule{0.2em}{0ex}}×\phantom{\dominion{0.2em}{0ex}}{10}^{-ii}{\phantom{\rule{0.2em}{0ex}}\text{m}}^{3}[/latex] at a pressure of [latex]2.0\phantom{\dominion{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{v}{\phantom{\rule{0.2em}{0ex}}\text{Northward/m}}^{2}.[/latex] (a) What is the temperature of the gas? (b) The gas undergoes a quasi-static adiabatic pinch until its book is decreased to [latex]5.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-3}{\phantom{\rule{0.2em}{0ex}}\text{m}}^{three}.[/latex] What is the new gas temperature? (c) How much work is done on the gas during the compression? (d) What is the change in the internal energy of the gas?

One mole of an ideal gas is initially in a chamber of volume [latex]1.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-2}{\phantom{\dominion{0.2em}{0ex}}\text{m}}^{iii}[/latex] and at a temperature of [latex]27\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]. (a) How much heat is absorbed past the gas when it slowly expands isothermally to twice its initial volume? (b) Suppose the gas is slowly transformed to the same final country past first decreasing the pressure at constant volume and so expanding it isobarically. What is the heat transferred for this case? (c) Calculate the oestrus transferred when the gas is transformed quasi-statically to the same terminal state past expanding it isobarically, so decreasing its pressure at constant volume.

Bear witness Solution

a. 1700 J; b. 1200 J; c. 2400 J

A bullet of mass 10 g is traveling horizontally at 200 thousand/s when it strikes and embeds in a pendulum bob of mass ii.0 kg. (a) How much mechanical energy is dissipated in the collision? (b) Assuming that [latex]{C}_{v}[/latex] for the bob plus bullet is 3R, calculate the temperature increase of the organisation due to the collision. Accept the molecular mass of the system to be 200 g/mol.

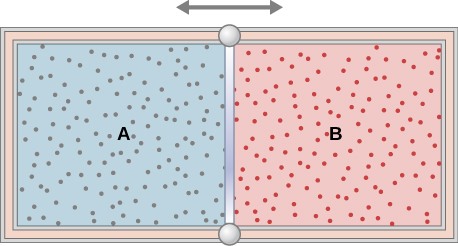
The insulated cylinder shown below is closed at both ends and contains an insulating piston that is costless to move on frictionless bearings. The piston divides the chamber into two compartments containing gases A and B. Originally, each compartment has a volume of [latex]5.0\phantom{\dominion{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-2}{\phantom{\rule{0.2em}{0ex}}\text{m}}^{3}[/latex] and contains a monatomic platonic gas at a temperature of [latex]0\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] and a pressure of 1.0 atm. (a) How many moles of gas are in each compartment? (b) Oestrus Q is slowly added to A so that information technology expands and B is compressed until the pressure of both gases is iii.0 atm. Use the fact that the compression of B is adiabatic to determine the final book of both gases. (c) What are their final temperatures? (d) What is the value of Q?

The figure is an illustration of a container with a partition in the middle dividing it into two chambers. A double headed horizontal arrow above the partition indicates that it is moveable The outer walls are insulated. The chamber on the left is labeled with an A, and is full of one gas, indicated by blue shading and many small dots representing the gas molecules. The right chamber is labeled with a B, and is full of a second gas, indicated by red shading and many small dots representing the gas molecules.

Testify Solution

a. 2.ii mol; b. [latex]{V}_{A}=two.six\phantom{\dominion{0.2em}{0ex}}×\phantom{\dominion{0.2em}{0ex}}{x}^{-2}{\text{m}}^{3}[/latex], [latex]{5}_{B}=7.4\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-ii}{\text{m}}^{three}[/latex]; c. [latex]{T}_{A}=1220\phantom{\rule{0.2em}{0ex}}\text{Grand},{T}_{B}=430\phantom{\rule{0.2em}{0ex}}\text{K}[/latex]; d. 30,500 J

In a diesel engine, the fuel is ignited without a spark plug. Instead, air in a cylinder is compressed adiabatically to a temperature above the ignition temperature of the fuel; at the point of maximum compression, the fuel is injected into the cylinder. Suppose that air at [latex]20\phantom{\dominion{0.2em}{0ex}}\text{°}\text{C}[/latex] is taken into the cylinder at a volume [latex]{V}_{1}[/latex] and so compressed adiabatically and quasi-statically to a temperature of [latex]600\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] and a book [latex]{V}_{ii}.[/latex] If [latex]\gamma =1.4,[/latex] what is the ratio [latex]{V}_{one}\text{/}{5}_{2}?[/latex] (Note: In an operating diesel engine, the compression is not quasi-static.)

Licenses and Attributions

Adiabatic Processes for an Ideal Gas. Authored past: OpenStax Higher. Located at: https://openstax.org/books/university-physics-book-ii/pages/3-vi-adiabatic-processes-for-an-platonic-gas. License: CC By: Attribution. License Terms: Download for gratuitous at https://openstax.org/books/university-physics-volume-2/pages/1-introduction

Is Helium An Ideal Gas,

Source: https://pressbooks.online.ucf.edu/osuniversityphysics2/chapter/adiabatic-processes-for-an-ideal-gas/

Posted by: holimansque1965.blogspot.com

0 Response to "Is Helium An Ideal Gas"

Post a Comment

Subscribe to: Post Comments (Atom)

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel