Inverse Of An Exponential Function

Mathematical office, denoted exp(x) or east^x

This commodity is nigh the function f(10) = east^x and its generalizations. For functions of the grade f(10) = 10^r , see Power function. For the bivariate function f(ten,y) = ten^y , meet Exponentiation. For the representation of scientific numbers, see E notation.

Exponential
The natural exponential function along part of the real axis
Full general information
Full general definition	${\displaystyle \exp z=e^{z}}$
Motivation of invention	Analytic proofs
Fields of application	Pure and applied mathematics
Domain, Codomain and Paradigm
Domain	${\displaystyle \mathbb {C} }$
Image	${\displaystyle {\brainstorm{cases}(0,\infty )&{\text{for }}z\in \mathbb {R} \\\mathbb {C} \setminus \{0\}&{\text{for }}z\in \mathbb {C} \end{cases}}}$
Specific values
At zero	1
Value at i	e
Specific features
Fixed point	−Due westn(−1) for ${\displaystyle n\in \mathbb {Z} }$
Related functions
Reciprocal	${\displaystyle \exp(-z)}$
Inverse	Complex logarithm ${\displaystyle \ln z,z\in \mathbb {R} }$
Derivative	${\displaystyle \exp 'z=\exp z}$
Antiderivative	${\displaystyle \int \exp z\,dz=\exp z+C}$
Series definition
Taylor series	${\displaystyle \exp z=\sum _{n=0}^{\infty }{\frac {z^{n}}{north!}}}$

Exponential functions with bases 2 and 1/2

The exponential role is a mathematical function denoted by ${\displaystyle f(x)=\exp(x)}$ or ${\displaystyle east^{x}}$ (where the argument ten is written as an exponent). Unless otherwise specified, the term more often than not refers to the positive-valued function of a existent variable, although it can exist extended to the circuitous numbers or generalized to other mathematical objects like matrices or Prevarication algebras. The exponential role originated from the notion of exponentiation (repeated multiplication), but mod definitions (in that location are several equivalent characterizations) allow information technology to be rigorously extended to all real arguments, including irrational numbers. Its ubiquitous occurrence in pure and applied mathematics led mathematician Walter Rudin to opine that the exponential office is "the well-nigh important function in mathematics".^[1]

The exponential function satisfies the exponentiation identity

$${\displaystyle due east^{x+y}=e^{x}e^{y}{\text{ for all }}x,y\in \mathbb {R} ,}$$

which, along with the definition ${\displaystyle e=\exp(i)}$ , shows that ${\displaystyle e^{n}=\underbrace {e\times \cdots \times due east} _{n{\text{ factors}}}}$ for positive integers n, and relates the exponential function to the elementary notion of exponentiation. The base of the exponential role, its value at i, ${\displaystyle eastward=\exp(1)}$ , is a ubiquitous mathematical constant chosen Euler's number.

While other continuous nonzero functions ${\displaystyle f:\mathbb {R} \to \mathbb {R} }$ that satisfy the exponentiation identity are also known as exponential functions, the exponential role exp is the unique real-valued role of a real variable whose derivative is itself and whose value at 0 is i; that is, ${\displaystyle \exp '(x)=\exp(x)}$ for all real ten, and ${\displaystyle \exp(0)=ane.}$ Thus, exp is sometimes chosen the natural exponential function to distinguish it from these other exponential functions, which are the functions of the grade ${\displaystyle f(ten)=ab^{x},}$ where the base b is a positive existent number. The relation ${\displaystyle b^{x}=e^{10\ln b}}$ for positive b and existent or complex x establishes a strong relationship between these functions, which explains this ambiguous terminology.

The real exponential role can likewise exist defined as a power series. This power series definition is readily extended to complex arguments to allow the complex exponential part ${\displaystyle \exp :\mathbb {C} \to \mathbb {C} }$ to be defined. The complex exponential function takes on all complex values except for 0 and is closely related to the complex trigonometric functions, as shown past Euler's formula.

Motivated by more abstract properties and characterizations of the exponential function, the exponential can be generalized to and defined for entirely different kinds of mathematical objects (for example, a foursquare matrix or a Lie algebra).

In applied settings, exponential functions model a human relationship in which a abiding change in the contained variable gives the same proportional change (that is, percentage increase or subtract) in the dependent variable. This occurs widely in the natural and social sciences, as in a self-reproducing population, a fund accruing compound interest, or a growing body of manufacturing expertise. Thus, the exponential function as well appears in a variety of contexts within physics, computer scientific discipline, chemistry, engineering, mathematical biology, and economic science.

The real exponential function is a bijection from ${\displaystyle \mathbb {R} }$ to ${\displaystyle (0;\infty )}$ .^[2] Its inverse function is the natural logarithm, denoted ${\displaystyle \ln ,}$ ^{[nb 1]} ${\displaystyle \log ,}$ ^{[nb 2]} or ${\displaystyle \log _{east};}$ because of this, some old texts^[3] refer to the exponential role as the antilogarithm.

Graph [edit]

The graph of ${\displaystyle y=e^{10}}$ is upward-sloping, and increases faster as 10 increases.^[4] The graph ever lies in a higher place the x-axis, but becomes arbitrarily close to it for big negative x; thus, the x-axis is a horizontal asymptote. The equation ${\displaystyle {\tfrac {d}{dx}}e^{x}=e^{x}}$ means that the slope of the tangent to the graph at each betoken is equal to its y-coordinate at that point.

Relation to more general exponential functions [edit]

The exponential part ${\displaystyle f(x)=e^{x}}$ is sometimes called the natural exponential part for distinguishing it from the other exponential functions. The study of whatsoever exponential function tin hands be reduced to that of the natural exponential function, since per definition, for positive b,

$${\displaystyle ab^{x}:=ae^{x\ln b}}$$

Every bit functions of a existent variable, exponential functions are uniquely characterized past the fact that the derivative of such a function is directly proportional to the value of the office. The constant of proportionality of this relationship is the natural logarithm of the base b:

$${\displaystyle {\frac {d}{dx}}b^{10}\ {\stackrel {\text{def}}{=}}\ {\frac {d}{dx}}due east^{x\ln(b)}=e^{x\ln(b)}\ln(b)=b^{x}\ln(b).}$$

For b > 1, the role ${\displaystyle b^{x}}$ is increasing (as depicted for b = e and b = ii), considering ${\displaystyle \ln b>0}$ makes the derivative always positive; while for b < ane, the function is decreasing (every bit depicted for b = 1 / two ); and for b = 1 the function is constant.

Euler's number due east = 2.71828... is the unique base for which the constant of proportionality is 1, since ${\displaystyle \ln(e)=1}$ , so that the function is its ain derivative:

$${\displaystyle {\frac {d}{dx}}e^{x}=e^{x}\ln(east)=e^{ten}.}$$

This part, besides denoted equally exp 10 , is called the "natural exponential function",^{[5] [half-dozen]} or merely "the exponential function". Since any exponential function can exist written in terms of the natural exponential as ${\displaystyle b^{ten}=e^{ten\ln b}}$ , it is computationally and conceptually user-friendly to reduce the written report of exponential functions to this particular one. The natural exponential is hence denoted by

$${\displaystyle x\mapsto eastward^{10}}$$

or

$${\displaystyle ten\mapsto \exp x.}$$

The former notation is ordinarily used for simpler exponents, while the latter is preferred when the exponent is a complicated expression.

For real numbers c and d, a part of the grade ${\displaystyle f(x)=ab^{cx+d}}$ is as well an exponential function, since information technology can be rewritten as

$${\displaystyle ab^{cx+d}=\left(ab^{d}\correct)\left(b^{c}\right)^{x}.}$$

Formal definition [edit]

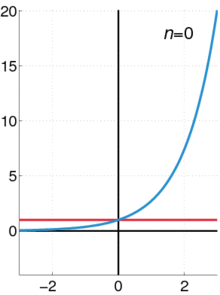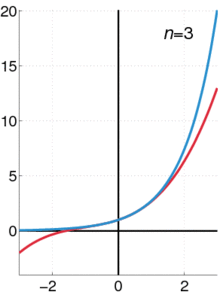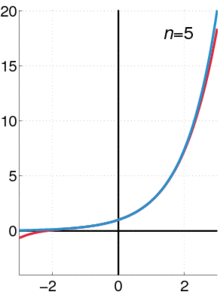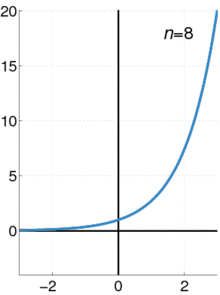
The exponential function (in blue), and the sum of the outset n + one terms of its power series (in red).

The real exponential office ${\displaystyle \exp \colon \mathbb {R} \to \mathbb {R} }$ tin be characterized in a diverseness of equivalent means. It is ordinarily defined past the following ability series:^{[1] [7]}

$${\displaystyle \exp ten:=\sum _{g=0}^{\infty }{\frac {10^{thousand}}{k!}}=1+x+{\frac {x^{2}}{2}}+{\frac {x^{three}}{six}}+{\frac {ten^{4}}{24}}+\cdots }$$

Since the radius of convergence of this power series is infinite, this definition is, in fact, applicable to all complex numbers ${\displaystyle z\in \mathbb {C} }$ (see § Complex airplane for the extension of ${\displaystyle \exp 10}$ to the complex plane). The constant e can and so be divers as ${\textstyle e=\exp ane=\sum _{k=0}^{\infty }(1/k!).}$

The term-by-term differentiation of this power series reveals that ${\textstyle {\frac {d}{dx}}\exp ten=\exp x}$ for all real x, leading to another common characterization of ${\displaystyle \exp x}$ equally the unique solution of the differential equation

$${\displaystyle y'(x)=y(10),}$$

satisfying the initial condition ${\displaystyle y(0)=1.}$

Based on this characterization, the chain rule shows that its inverse function, the natural logarithm, satisfies ${\textstyle {\frac {d}{dy}}\log _{e}y=1/y}$ for ${\displaystyle y>0,}$ or ${\textstyle \log _{eastward}y=\int _{1}^{y}{\frac {dt}{t}}\,.}$ This relationship leads to a less mutual definition of the real exponential function ${\displaystyle \exp x}$ as the solution ${\displaystyle y}$ to the equation

$${\displaystyle x=\int _{one}^{y}{\frac {1}{t}}\,dt.}$$

Past style of the binomial theorem and the power series definition, the exponential function can likewise exist defined every bit the following limit:^{[8] [7]}

$${\displaystyle \exp 10=\lim _{due north\to \infty }\left(1+{\frac {ten}{n}}\right)^{n}.}$$

Information technology can be shown that every continuous, nonzero solution of the functional equation ${\displaystyle f(x+y)=f(x)f(y)}$ is an exponential function, ${\displaystyle f:\mathbb {R} \to \mathbb {R} ,\ x\mapsto e^{kx},}$ with ${\displaystyle thousand\in \mathbb {R} .}$

Overview [edit]

The red curve is the exponential function. The black horizontal lines show where information technology crosses the green vertical lines.

The exponential function arises whenever a quantity grows or decays at a charge per unit proportional to its current value. One such situation is continuously compounded interest, and in fact it was this observation that led Jacob Bernoulli in 1683^[nine] to the number

$${\displaystyle \lim _{n\to \infty }\left(1+{\frac {1}{north}}\right)^{n}}$$

now known as e . Later on, in 1697, Johann Bernoulli studied the calculus of the exponential function.^[9]

If a principal corporeality of ane earns interest at an almanac rate of x compounded monthly, and so the involvement earned each month is x / 12 times the current value, then each month the total value is multiplied by (1 + ten / 12 ), and the value at the finish of the year is (1 + x / 12 )¹² . If instead involvement is compounded daily, this becomes (1 + 10 / 365 )³⁶⁵ . Letting the number of time intervals per year grow without bound leads to the limit definition of the exponential function,

$${\displaystyle \exp x=\lim _{n\to \infty }\left(one+{\frac {x}{due north}}\right)^{northward}}$$

commencement given by Leonhard Euler.^[8] This is one of a number of characterizations of the exponential function; others involve serial or differential equations.

From any of these definitions it can be shown that the exponential function obeys the bones exponentiation identity,

$${\displaystyle \exp(ten+y)=\exp x\cdot \exp y}$$

which justifies the notation e ¹⁰ for exp 10 .

The derivative (rate of change) of the exponential function is the exponential function itself. More than generally, a function with a rate of change proportional to the function itself (rather than equal to it) is expressible in terms of the exponential function. This function property leads to exponential growth or exponential disuse.

The exponential function extends to an entire function on the complex aeroplane. Euler's formula relates its values at purely imaginary arguments to trigonometric functions. The exponential function also has analogues for which the statement is a matrix, or even an element of a Banach algebra or a Lie algebra.

Derivatives and differential equations [edit]

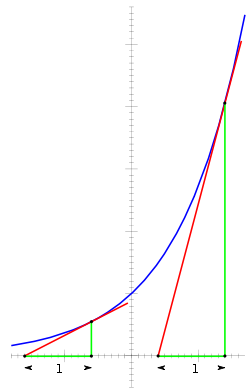
The derivative of the exponential function is equal to the value of the function. From any point P on the bend (bluish), allow a tangent line (crimson), and a vertical line (green) with height h be drawn, forming a right triangle with a base b on the x -axis. Since the slope of the crimson tangent line (the derivative) at P is equal to the ratio of the triangle'southward height to the triangle's base (rise over run), and the derivative is equal to the value of the function, h must be equal to the ratio of h to b . Therefore, the base b must e'er be one.

The importance of the exponential office in mathematics and the sciences stems mainly from its holding equally the unique role which is equal to its derivative and is equal to one when x = 0. That is,

$${\displaystyle {\frac {d}{dx}}e^{x}=e^{x}\quad {\text{and}}\quad e^{0}=1.}$$

Functions of the form ce ^x for abiding c are the just functions that are equal to their derivative (past the Picard–Lindelöf theorem). Other means of proverb the same matter include:

• The gradient of the graph at any signal is the acme of the function at that point.
• The rate of increase of the function at ten is equal to the value of the function at 10 .
• The function solves the differential equation y′ = y .
• exp is a fixed point of derivative as a functional.

If a variable'south growth or decay rate is proportional to its size—as is the case in unlimited population growth (see Malthusian catastrophe), continuously compounded interest, or radioactive decay—and so the variable can be written as a constant times an exponential office of time. Explicitly for any real constant k , a function f: R → R satisfies f′ = kf if and just if f(x) = ce ^kx for some constant c . The constant k is called the decay constant, disintegration constant,^[ten] rate constant,^[11] or transformation constant.^[12]

Furthermore, for any differentiable function f , we find, by the chain dominion:

$${\displaystyle {\frac {d}{dx}}due east^{f(x)}=f'(x)e^{f(x)}.}$$

Continued fractions for e ^x [edit]

A connected fraction for east ^x can be obtained via an identity of Euler:

$${\displaystyle e^{ten}=1+{\cfrac {x}{i-{\cfrac {ten}{x+2-{\cfrac {2x}{ten+3-{\cfrac {3x}{x+4-\ddots }}}}}}}}}$$

The post-obit generalized continued fraction for east ^z converges more rapidly:^[13]

$${\displaystyle e^{z}=i+{\cfrac {2z}{2-z+{\cfrac {z^{2}}{6+{\cfrac {z^{2}}{x+{\cfrac {z^{2}}{fourteen+\ddots }}}}}}}}}$$

or, by applying the substitution z = x / y :

$${\displaystyle east^{\frac {x}{y}}=ane+{\cfrac {2x}{2y-ten+{\cfrac {x^{2}}{6y+{\cfrac {10^{2}}{10y+{\cfrac {ten^{ii}}{14y+\ddots }}}}}}}}}$$

with a special case for z = two:

$${\displaystyle e^{ii}=ane+{\cfrac {four}{0+{\cfrac {2^{ii}}{half dozen+{\cfrac {2^{two}}{10+{\cfrac {two^{two}}{14+\ddots \,}}}}}}}}=vii+{\cfrac {ii}{v+{\cfrac {one}{7+{\cfrac {1}{ix+{\cfrac {1}{11+\ddots \,}}}}}}}}}$$

This formula also converges, though more slowly, for z > 2. For example:

$${\displaystyle e^{3}=i+{\cfrac {6}{-1+{\cfrac {iii^{2}}{6+{\cfrac {3^{2}}{10+{\cfrac {3^{two}}{xiv+\ddots \,}}}}}}}}=13+{\cfrac {54}{7+{\cfrac {nine}{14+{\cfrac {9}{18+{\cfrac {9}{22+\ddots \,}}}}}}}}}$$

Complex airplane [edit]

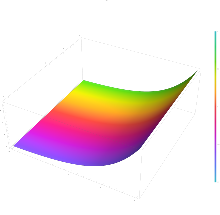
The exponential function e^z plotted in the complex airplane from -2-2i to 2+2i

As in the existent example, the exponential function can be defined on the complex plane in several equivalent forms. The most common definition of the complex exponential role parallels the power serial definition for real arguments, where the real variable is replaced by a circuitous i:

$${\displaystyle \exp z:=\sum _{k=0}^{\infty }{\frac {z^{k}}{k!}}}$$

Alternatively, the complex exponential function may be defined past modelling the limit definition for existent arguments, merely with the real variable replaced past a circuitous one:

$${\displaystyle \exp z:=\lim _{n\to \infty }\left(ane+{\frac {z}{n}}\right)^{due north}}$$

For the power series definition, term-wise multiplication of two copies of this ability series in the Cauchy sense, permitted by Mertens' theorem, shows that the defining multiplicative property of exponential functions continues to concur for all circuitous arguments:

$${\displaystyle \exp(westward+z)=\exp w\exp z{\text{ for all }}w,z\in \mathbb {C} }$$

The definition of the circuitous exponential function in turn leads to the advisable definitions extending the trigonometric functions to circuitous arguments.

In particular, when z = information technology (t real), the series definition yields the expansion

$${\displaystyle \exp(information technology)=\left(i-{\frac {t^{ii}}{2!}}+{\frac {t^{4}}{4!}}-{\frac {t^{6}}{6!}}+\cdots \right)+i\left(t-{\frac {t^{3}}{iii!}}+{\frac {t^{v}}{five!}}-{\frac {t^{7}}{7!}}+\cdots \right).}$$

In this expansion, the rearrangement of the terms into real and imaginary parts is justified past the absolute convergence of the series. The real and imaginary parts of the above expression in fact correspond to the series expansions of cos t and sin t , respectively.

This correspondence provides motivation for defining cosine and sine for all complex arguments in terms of ${\displaystyle \exp(\pm iz)}$ and the equivalent ability series:^[fourteen]

$${\displaystyle {\brainstorm{aligned}&\cos z:={\frac {\exp(iz)+\exp(-iz)}{2}}=\sum _{thou=0}^{\infty }(-1)^{k}{\frac {z^{2k}}{(2k)!}},\\[5pt]{\text{and }}\quad &\sin z:={\frac {\exp(iz)-\exp(-iz)}{2i}}=\sum _{m=0}^{\infty }(-1)^{1000}{\frac {z^{2k+1}}{(2k+1)!}}\end{aligned}}}$$

for all ${\textstyle z\in \mathbb {C} .}$

The functions exp, cos, and sin and so defined have infinite radii of convergence by the ratio exam and are therefore entire functions (that is, holomorphic on ${\displaystyle \mathbb {C} }$ ). The range of the exponential office is ${\displaystyle \mathbb {C} \setminus \{0\}}$ , while the ranges of the complex sine and cosine functions are both ${\displaystyle \mathbb {C} }$ in its entirety, in accord with Picard'southward theorem, which asserts that the range of a nonconstant unabridged part is either all of ${\displaystyle \mathbb {C} }$ , or ${\displaystyle \mathbb {C} }$ excluding one lacunary value.

These definitions for the exponential and trigonometric functions pb trivially to Euler's formula:

$${\displaystyle \exp(iz)=\cos z+i\sin z{\text{ for all }}z\in \mathbb {C} .}$$

We could alternatively ascertain the complex exponential function based on this relationship. If z = ten + iy , where x and y are both real, and so nosotros could define its exponential every bit

$${\displaystyle \exp z=\exp(x+iy):=(\exp x)(\cos y+i\sin y)}$$

where exp, cos, and sin on the right-hand side of the definition sign are to be interpreted as functions of a real variable, previously defined by other means.^[15]

For ${\displaystyle t\in \mathbb {R} }$ , the relationship ${\displaystyle {\overline {\exp(it)}}=\exp(-it)}$ holds, so that ${\displaystyle \left|\exp(it)\right|=1}$ for real ${\displaystyle t}$ and ${\displaystyle t\mapsto \exp(it)}$ maps the real line (modern twoπ ) to the unit circle in the complex plane. Moreover, going from ${\displaystyle t=0}$ to ${\displaystyle t=t_{0}}$ , the curve defined past ${\displaystyle \gamma (t)=\exp(it)}$ traces a segment of the unit circumvolve of length

$${\displaystyle \int _{0}^{t_{0}}|\gamma '(t)|\,dt=\int _{0}^{t_{0}}|i\exp(it)|\,dt=t_{0},}$$

starting from z = 1 in the complex plane and going counterclockwise. Based on these observations and the fact that the measure of an angle in radians is the arc length on the unit circle subtended past the angle, information technology is piece of cake to run across that, restricted to existent arguments, the sine and cosine functions equally divers above coincide with the sine and cosine functions as introduced in unproblematic mathematics via geometric notions.

The complex exponential role is periodic with period 2πi and ${\displaystyle \exp(z+2\pi ik)=\exp z}$ holds for all ${\displaystyle z\in \mathbb {C} ,k\in \mathbb {Z} }$ .

When its domain is extended from the real line to the complex plane, the exponential function retains the post-obit properties:

$${\displaystyle {\brainstorm{aligned}&e^{z+w}=e^{z}e^{w}\,\\[5pt]&eastward^{0}=one\,\\[5pt]&e^{z}\neq 0\\[5pt]&{\frac {d}{dz}}e^{z}=e^{z}\\[5pt]&\left(eastward^{z}\right)^{north}=due east^{nz},due north\in \mathbb {Z} \finish{aligned}}}$$

for all ${\textstyle w,z\in \mathbb {C} .}$

Extending the natural logarithm to circuitous arguments yields the complex logarithm log z , which is a multivalued part.

We can then define a more general exponentiation:

$${\displaystyle z^{due west}=east^{w\log z}}$$

for all complex numbers z and west . This is also a multivalued function, even when z is real. This distinction is problematic, every bit the multivalued functions log z and z ^w are easily confused with their single-valued equivalents when substituting a existent number for z . The rule almost multiplying exponents for the example of positive real numbers must be modified in a multivalued context:

(e^z ) ^w
≠ e^zw , but rather (eastward^z ) ^{due west}
= e ^{(z + 2niπ)w} multivalued over integers n

Run across failure of power and logarithm identities for more than about issues with combining powers.

The exponential function maps whatsoever line in the complex plane to a logarithmic spiral in the complex airplane with the center at the origin. Two special cases exist: when the original line is parallel to the real axis, the resulting spiral never closes in on itself; when the original line is parallel to the imaginary axis, the resulting spiral is a circumvolve of some radius.

• 3D plots of real part, imaginary role, and modulus of the exponential part

• 

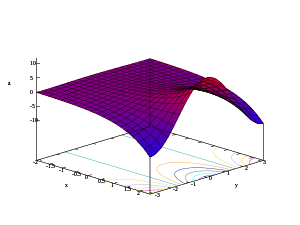
  z = Re(e ^{x + iy} )

• 

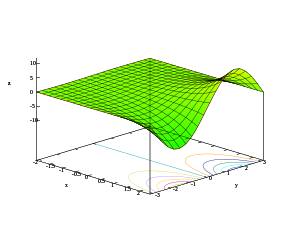
  z = Im(east ^{x + iy} )

• 

  z = | e ^{ten + iy} |

Considering the complex exponential office as a function involving iv existent variables:

$${\displaystyle v+iw=\exp(10+iy)}$$

the graph of the exponential office is a two-dimensional surface curving through four dimensions.

Starting with a color-coded portion of the ${\displaystyle xy}$ domain, the post-obit are depictions of the graph as variously projected into two or three dimensions.

• Graphs of the complex exponential function

• 

  Project onto the range circuitous plane (V/W). Compare to the adjacent, perspective picture show.

• 

  Project into the ${\displaystyle x}$ , ${\displaystyle v}$ , and ${\displaystyle w}$ dimensions, producing a flared horn or funnel shape (envisioned every bit 2-D perspective image).

The second prototype shows how the domain complex aeroplane is mapped into the range complex plane:

The tertiary and quaternary images show how the graph in the second image extends into one of the other 2 dimensions not shown in the second epitome.

The third epitome shows the graph extended along the real ${\displaystyle 10}$ axis. It shows the graph is a surface of revolution about the ${\displaystyle x}$ centrality of the graph of the real exponential function, producing a horn or funnel shape.

The 4th image shows the graph extended along the imaginary ${\displaystyle y}$ axis. It shows that the graph'southward surface for positive and negative ${\displaystyle y}$ values doesn't actually meet forth the negative existent ${\displaystyle v}$ axis, just instead forms a screw surface about the ${\displaystyle y}$ axis. Considering its ${\displaystyle y}$ values accept been extended to ±2π , this image likewise better depicts the 2π periodicity in the imaginary ${\displaystyle y}$ value.

Computation of a ^b where both a and b are circuitous [edit]

Complex exponentiation a ^b can be divers by converting a to polar coordinates and using the identity (e ^{ln a} ) ^b
= a ^b :

$${\displaystyle a^{b}=\left(re^{\theta i}\right)^{b}=\left(e^{(\ln r)+\theta i}\right)^{b}=e^{\left((\ln r)+\theta i\right)b}}$$

However, when b is non an integer, this function is multivalued, because θ is not unique (run into failure of ability and logarithm identities).

Matrices and Banach algebras [edit]

The ability series definition of the exponential role makes sense for square matrices (for which the function is called the matrix exponential) and more generally in any unital Banach algebra B . In this setting, east ⁰ = 1, and eastward ^x is invertible with inverse e ⁻¹⁰ for any x in B . If xy = yx , then e ^{x + y} = e ^x due east ^y , just this identity tin can fail for noncommuting x and y .

Some culling definitions pb to the aforementioned function. For instance, e ^x can exist divers as

$${\displaystyle \lim _{due north\to \infty }\left(1+{\frac {x}{n}}\right)^{n}.}$$

Or e ^x tin can be defined as f _ten (1), where f _x  : R → B is the solution to the differential equation df_ten / dt (t) = tenf _x (t), with initial condition f _x (0) = one; it follows that f _x (t) = e ^tx for every t in R .

Lie algebras [edit]

Given a Lie grouping M and its associated Lie algebra ${\displaystyle {\mathfrak {g}}}$ , the exponential map is a map ${\displaystyle {\mathfrak {g}}}$ ↦ Yard satisfying similar backdrop. In fact, since R is the Prevarication algebra of the Lie group of all positive real numbers under multiplication, the ordinary exponential role for real arguments is a special case of the Lie algebra situation. Similarly, since the Lie group GL(northward,R) of invertible n × n matrices has every bit Prevarication algebra M(n,R), the infinite of all n × n matrices, the exponential part for square matrices is a special example of the Lie algebra exponential map.

The identity exp(x + y) = exp ten exp y can neglect for Prevarication algebra elements x and y that do not commute; the Baker–Campbell–Hausdorff formula supplies the necessary correction terms.

Transcendency [edit]

The office eastward ^z is non in C(z) (that is, is non the quotient of two polynomials with circuitous coefficients).

If a ₁, ..., a _northward are distinct complex numbers, then east ^{a ₁ z} , ..., e ^{a _northward z} are linearly independent over C(z). It follows that e ^z is transcendental over C(z).

Computation [edit]

When computing (an approximation of) the exponential function near the statement 0, the result will be close to 1, and computing the value of the difference ${\displaystyle eastward^{x}-1}$ with floating-point arithmetic may pb to the loss of (possibly all) significant figures, producing a big calculation error, peradventure even a meaningless consequence.

Post-obit a proposal by William Kahan, information technology may thus be useful to have a dedicated routine, often chosen expm1, for computing e^ten − i directly, bypassing computation of e ^ten . For example, if the exponential is computed by using its Taylor series

$${\displaystyle e^{10}=1+10+{\frac {x^{2}}{ii}}+{\frac {x^{iii}}{six}}+\cdots +{\frac {x^{n}}{n!}}+\cdots ,}$$

one may apply the Taylor series of ${\displaystyle eastward^{x}-1}$ :

$${\displaystyle e^{10}-i=x+{\frac {10^{2}}{2}}+{\frac {10^{3}}{6}}+\cdots +{\frac {x^{north}}{n!}}+\cdots .}$$

This was first implemented in 1979 in the Hewlett-Packard HP-41C figurer, and provided past several calculators,^{[sixteen] [17]} operating systems (for example Berkeley UNIX 4.3BSD^[18]), computer algebra systems, and programming languages (for example C99).^[19]

In addition to base due east , the IEEE 754-2008 standard defines similar exponential functions virtually 0 for base two and 10: ${\displaystyle 2^{ten}-1}$ and ${\displaystyle ten^{x}-1}$ .

A similar approach has been used for the logarithm (see lnp1).^{[nb iii]}

An identity in terms of the hyperbolic tangent,

$${\displaystyle \operatorname {expm1} (ten)=e^{10}-1={\frac {2\tanh(x/two)}{1-\tanh(x/ii)}},}$$

gives a high-precision value for small values of x on systems that do not implement expm1(x).

Alternatively, this expression can be used:^[xx]

${\displaystyle eastward^{x}-1=\lim _{n\to \infty }{\frac {x}{northward}}\sum _{k=1}^{northward}\left(1+{\frac {1}{north}}\right)^{kx}}$

Meet also [edit]

• Carlitz exponential, a feature p analogue
• Double exponential function – Exponential role of an exponential function
• Exponential field – Mathematical field with an extra operation
• Gaussian part
• One-half-exponential function, a compositional square root of an exponential office
• List of exponential topics
• List of integrals of exponential functions
• Mittag-Leffler function, a generalization of the exponential office
• p -adic exponential office
• Padé table for exponential function – Padé approximation of exponential part by a fraction of polynomial functions
• Tetration – Repeated or iterated exponentiation

Notes [edit]

1. ^ The notation ln x is the ISO standard and is prevalent in the natural sciences and secondary didactics (US). However, some mathematicians (for example, Paul Halmos) have criticized this notation and adopt to use log x for the natural logarithm of x.
2. ^ In pure mathematics, the notation log ten generally refers to the natural logarithm of ten or a logarithm in general if the base is immaterial.
3. ^ A like approach to reduce round-off errors of calculations for certain input values of trigonometric functions consists of using the less mutual trigonometric functions versine, vercosine, coversine, covercosine, haversine, havercosine, hacoversine, hacovercosine, exsecant and excosecant.

References [edit]

1. ^ ^{a b} Rudin, Walter (1987). Real and complex analysis (3rd ed.). New York: McGraw-Hill. p. one. ISBN978-0-07-054234-ane.
2. ^ Meier, John; Smith, Derek (2017-08-07). Exploring Mathematics. Cambridge University Press. p. 167. ISBN978-1-107-12898-9.
3. ^ Converse, Henry Augustus; Durell, Fletcher (1911). Airplane and Spherical Trigonometry. Durell's mathematical series. C. E. Merrill Company. p. 12. Changed Use of a Table of Logarithms; that is, given a logarithm, to find the number corresponding to it, (called its antilogarithm) ... [1]
4. ^ "Exponential Function Reference". www.mathsisfun.com . Retrieved 2020-08-28 .
5. ^ Goldstein, Larry Joel; Lay, David C.; Schneider, David I.; Asmar, Nakhle H. (2006). Brief calculus and its applications (11th ed.). Prentice–Hall. ISBN978-0-13-191965-5. (467 pages)
6. ^ Courant; Robbins (1996). Stewart (ed.). What is Mathematics? An Elementary Approach to Ideas and Methods (2nd revised ed.). Oxford University Printing. p. 448. ISBN978-0-13-191965-five. This natural exponential function is identical with its derivative. This is actually the source of all the properties of the exponential part, and the basic reason for its importance in applications…
7. ^ ^{a b} Weisstein, Eric West. "Exponential Function". mathworld.wolfram.com . Retrieved 2020-08-28 .
8. ^ ^{a b} Maor, Eli. due east: the Story of a Number. p. 156.
9. ^ ^{a b} O'Connor, John J.; Robertson, Edmund F. (September 2001). "The number east". School of Mathematics and Statistics. University of St Andrews, Scotland. Retrieved 2011-06-thirteen .
10. ^ Serway, Raymond A.; Moses, Clement J.; Moyer, Curt A. (1989). Mod Physics. Fort Worth: Harcourt Caryatid Jovanovich. p. 384. ISBN0-03-004844-3.
11. ^ Simmons, George F. (1972). Differential Equations with Applications and Historical Notes. New York: McGraw-Hill. p. fifteen. LCCN 75173716.
12. ^ McGraw-Hill Encyclopedia of Science & Technology (10th ed.). New York: McGraw-Loma. 2007. ISBN978-0-07-144143-8.
13. ^ Lorentzen, L.; Waadeland, H. (2008). "A.2.2 The exponential part.". Connected Fractions. Atlantis Studies in Mathematics. Vol. 1. p. 268. doi:10.2991/978-94-91216-37-four. ISBN978-94-91216-37-iv.
14. ^ Rudin, Walter (1976). Principles of Mathematical Assay. New York: McGraw-Colina. p. 182. ISBN978-0-07-054235-8.
15. ^ Apostol, Tom M. (1974). Mathematical Assay (2nd ed.). Reading, Mass.: Addison Wesley. pp. 19. ISBN978-0-201-00288-1.
16. ^ HP 48G Series – Advanced User's Reference Manual (AUR) (4 ed.). Hewlett-Packard. December 1994 [1993]. HP 00048-90136, 0-88698-01574-2. Retrieved 2015-09-06 .
17. ^ HP 50g / 49g+ / 48gII graphing calculator advanced user's reference manual (AUR) (two ed.). Hewlett-Packard. 2009-07-xiv [2005]. HP F2228-90010. Retrieved 2015-10-ten . [2]
18. ^ Beebe, Nelson H. F. (2017-08-22). "Affiliate x.2. Exponential near zero". The Mathematical-Function Computation Handbook - Programming Using the MathCW Portable Software Library (one ed.). Salt Lake City, UT, Usa: Springer International Publishing AG. pp. 273–282. doi:10.1007/978-iii-319-64110-2. ISBN978-3-319-64109-vi. LCCN 2017947446. S2CID 30244721. Berkeley UNIX iv.3BSD introduced the expm1() function in 1987.
19. ^ Beebe, Nelson H. F. (2002-07-09). "Ciphering of expm1 = exp(x)−ane" (PDF). i.00. Table salt Lake Metropolis, Utah, USA: Section of Mathematics, Center for Scientific Computing, University of Utah. Retrieved 2015-11-02 .
20. ^ "Calculus - A limit calculation using Riemann integral".

External links [edit]

• "Exponential part", Encyclopedia of Mathematics, Ems Press, 2001 [1994]

Inverse Of An Exponential Function,

Source: https://en.wikipedia.org/wiki/Exponential_function

Posted by: holimansque1965.blogspot.com

Share this post